项目概览:
本项目通过构建多因子模型实现了沪深300指数增强策略,流程包括原始数据获取、因子生成、因子预处理、单因子检验、收益预测模型及风险模型等,具体流程如图:
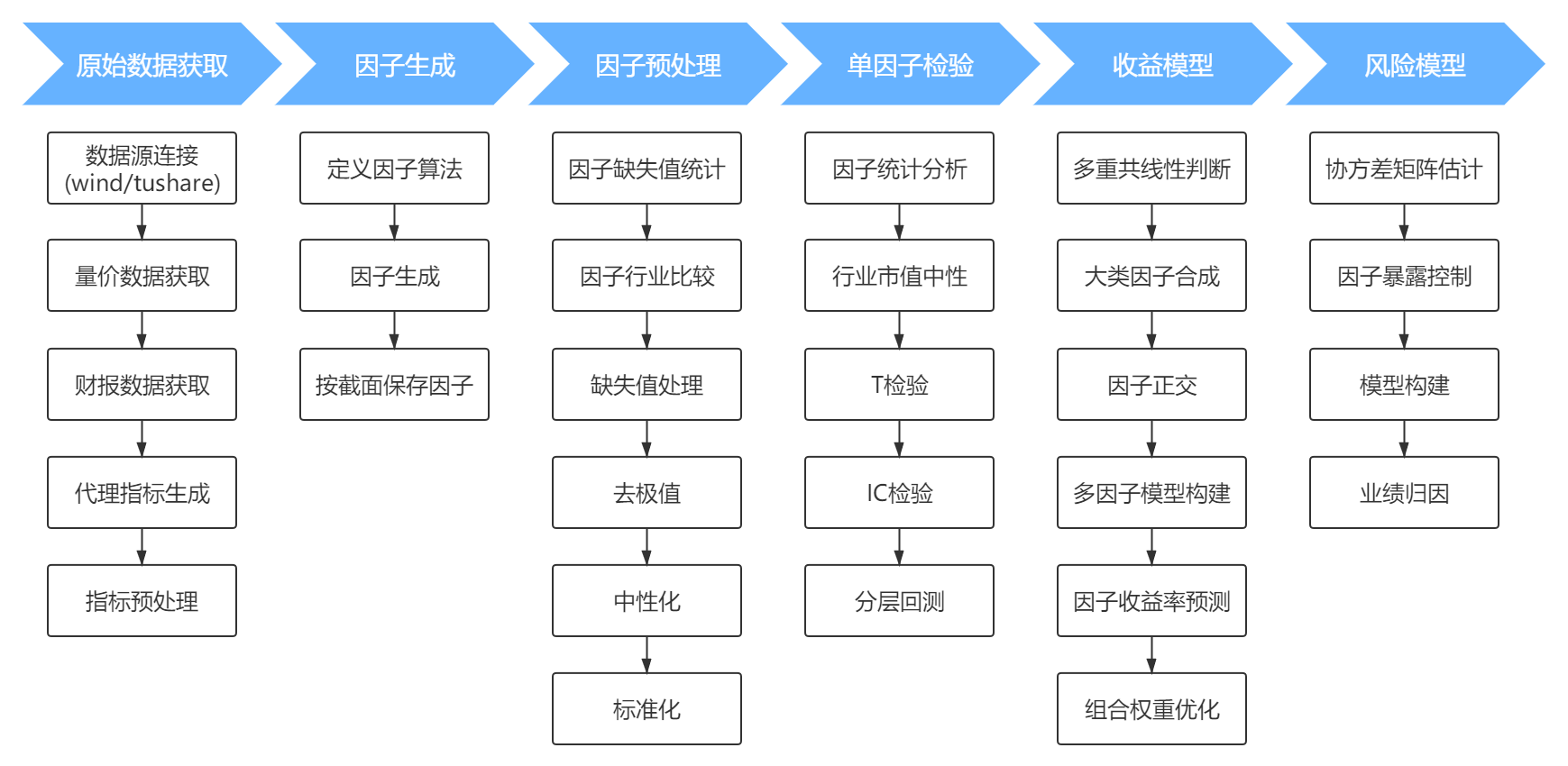
代码框架:
1.raw_data_fetch.py/原始数据获取.py:原始数据获取功能文件,用于从wind/tushare数据源获取原始数据,生成代理指标,数据以指标名作为文件名保存到磁盘文件中。
2.factor_generate.py/因子生成.py:因子生成功能文件,用于通过对各种指标的计算生成相应各种因子,因子最终以截面形式保存到文件。
3.factor_preprocess.py/因子预处理.py:因子预处理功能文件,用于对计算后的原始因子数据进行预处理,包括缺失值处理、中位数法去极值、标准化及相对行业和市值中性化处理。
4.single_factor_test.py/单因子检验.py:单因子检验功能文件,同时实现回测功能模块,用于对预处理后的因子逐个进行回归,IC检验、T检验、分层回测,对有效因子进行初步筛选。
5.index_enhance.py/指数增强模型.py:指数增强模型功能文件,用于对有效因子进行因子合成与正交,进行收益预测,并通过风险模型进行权重优化,然后利用回测引擎进行回测,生成回测报告,最后对结果进行业绩归因。
本模型针对沪深300成分股,最终选取估值因子、动量因子、流动性因子、成长因子、作为阿尔法因子,选取波动率因子、市值因子、 Beta 因子和行业因子作为风险因子,采用月频方式调仓,根据历史月频横截面回归计算因子收益率,并在每个月末根据最新的因子暴露预测下个月全部指数成分股收益,并通过风险模型以最大化组合的预测收益为目标,同时控制组合相对基准指数的行业及市值暴露,实现对组合中个股的权重优化,以沪深300增强为例,每个月通过模型从300只成分股中选出约60-100只个股,以最优权重构建组合。
回测周期为2014年1月 - 2019 年12月。模型采用 24 个月指数加权方式预测T+1期因子收益率,并进行市值中性化和行业中性化处理。经过回测,模型年化超额收益 8.3%,并在 2014-2019年 期间每一年都跑赢指数,平均跟踪误差 6.2%,平均双边换手率 12 倍。
多因子模型构建步骤:
一.因子生成
通过原始数据及指标生成各种因子,其中主要的关注点是财务指标的生成,一定要防止使用未来数据,财报数据需要进行数据对齐,因为各上市公司财报的发布日期之间不一定都是同一天,为避免前视偏差,在提取数据的时候需要对日期进行修正,保证因子数据为当时那个时刻所能获取的最新财报数据。
二.数据预处理 原始因子数据需经过缺失值处理、去极值、中性化、标准化等步骤后,才能进行下一步的单因子检验。
1.缺失值处理:原始因子会因为各种原因出现缺失值,当缺失值少于比如10%的情况下,可以使用行业中位数代替,但是如果缺失值过多,那么最好更换数据源或使用其他因子。
2.去极值:使用“中位数去极值法”,将超过上下限的极端值用上下限值代替,这样可以尽量防止极端值对回归产生过多影响。
3.标准化:不同因子量纲不同,为了使其具有可比性,需要对其进行 ZScore标准化处理,使因子序列近似成为一个符合N(0,1)正态分布的序列。
4.行业市值中性化:为了剔除数据中多余的风险暴露,防止投资组合过于集中,将因子序列对流动市值与行业哑变量做线性回归,取残差作为新的因子值。
三.单因子检验
单因子检测一般分为两种方式,一种是偏数学的统计检验法,另外一种是偏实际的分层回测法,两种方法可以结合使用互相印证。
1.统计检验法
依据Barra 手册中关于因子显著性测试的内容,对因子进行横截面回归,同时需要考虑行业与市值的影响。而IC( Information Coefficient)是衡量因子收益预测能力的重要参数,它 的计算方法是将每一期的因子值作为因变量,与行业哑变量和市值变量进行回归,取其残差,作为剔除行业与市值影响后的因子值。再计算新因子值与下一期股票收益序列间的 Spearman 相关系数。
评估指标说明:
IC>0 概率:衡量模型预测收益方向性是否一致的指标;
IRIC: IC 平均值/IC 标准差;
IC 平均值:衡量模型预测能力的指标; IC 标准差:衡量模型预测能力是否稳定的指标;
t 值绝对值>2 概率:衡量因子显著性是否稳定;
t 值绝对值平均值:衡量因子整体显著性的指标;
因子收益>0 概率:衡量因子收益率方向性是否一致的指标;
因子收益 t 值:衡量因子收益率统计上是否显著不为 0 的指标;
因子收益平均值:衡量因子收益能力大小的指标;
因子收益标准差:衡量因子收益能力波动率的指标;
最终可以依据以上每个因子的评估指标选出合适的因子,比如t 值绝对值平均值大于2,ICIR稳定的因子等。
2.分层回测法
在每个截面期的最后一个交易日,提取样本内股票因子值,并剔除因子值缺失的 股票。按照因子将样本内股票排序,并按照序号从大到小平均分为 5 组,当然也可以分成10组。在下一个截面期的首个交易日,以当天的收盘价换仓并剔除当天因停牌等因素不能交易的股票。 对 5 组股票的历史收益率进行回测,并计算其年化收益率、波动率、夏普比率等值。然后查看每一组的股票收益率是否有较好的分层单调性,判断因子是否在截面上对股票有很好的区分能力。
四.指数增强策略构建
虽然上一步我们已经选出了在主观上与收益率有显著关系的因子池,但因子彼此之间(尤其是同一大类下所属的因子)有可能存在很强的相关性。这就是多重共线性问题,它会对投资组合有很不利的影响。因此有必要对因子进行大类因子合成以及因子正交,如果不做处理,投资组合会在同种因子类型上暴露过多风险,这种多重共线性问题会导致多元线性回归的结果偏差。一般在具体处理上可以有多种方法,比如对非常相似的因子可选取单因子检验效果最好的因子进入模型,剔除其他因子,也可以利用等权法、历史收益率加权法、 ICIR加权法等处理手段,对因子进行合并,生成新的因子。因子正交也有施密特正交、规范正交和对称正交等。
接下来开始计算每一期的因子收益率,因子收益率的估计可以通过横截面回归得到(可以参考Barra模型),使用下一期个股收益率对上一期个股因子暴露进行回归,回归系数即为因子收益率。为解决异方差性,使用了WLS加权最小二乘法进行回归。
接下来开始计算个股收益率,股票收益率可以表示为市场收益率、行业收益率、风格收益率、阿尔法因子收益率以及特质收益率的线性组合。
得到所有因子的历史收益率序列后,就可以去估计T+1期因子预期收益率了,当然估计的方法有很多种,比如历史数据平均法,指数加权移动平均法,ARMA,ARCH,GARCH,滤波,神经网络等等,这里我采样窗口期为24个月的指数加权移动平均法来估计。然后通过因子预期收益率就可以计算出个股预期收益率。
最后以波动率因子、市值因子、Beta 因子、行业因子等作为风险因子,加上行业中性约束,市值中性约束等通过动态规划的方法计算出每期的股票最优权重。
最后为了弄明白组合收益究竟来自哪些因子,而哪些因素又会对组合收益产生不利影响,我们需要对组合进行业绩归因。当然业绩归因的方法也有很多种,比如多因子模型归因,比如Brinson模型归因等等。
策略信息如下:
回测时间: 2014年1月-2019年12月;
基准指数: 沪深300;
选股空间: 沪深300指数成份股(剔除ST 股票、剔除调仓时停牌股票、剔除每月停牌超过10天的股票);
交易成本:暂不考虑交易成本;
调仓频率:月频,每月第一个交易日;
调仓价格:收盘价;
行业及市值约束:行业、市值相对于基准的暴露为 0;
策略回测从2014年1月起,每个月初从沪深300成分股中选出约60-100只个股,构建投资组合,其年化超额收益为8.3%,每一年都能跑赢指数,平均跟踪误差为6.2%。当然这还仅仅只是基础的研究,所谓研究无止境,勇攀更高峰。这些年量化领域的竞争日趋激烈,多因子模型应该是其中最为成熟的方法论,它即是科学也是艺术,我们通过前人埋下的基石谨慎的前行,才能走的更远,走的更好。致广大而尽精微,极高明而道中庸。
项目代码: https://github.com/phonegapX/alphasickle