今天有空看了一下C语言(以VC6为具体实现平台)中的随机数的实现,我们先看一个例子:
其中RAND_MAX是一个宏, 值等于 0x7fff, 十进制的32767,这个值是C语言中short类型的最大值. srand是初始化随机数种子(seed)的函数,是以当前时间(time(NULL))为参数, 那随机数种子是什么东西, 为什么要以当前时间为参数, 带着这些问题我们再看一个例子:
这个例子的输出结果如图:
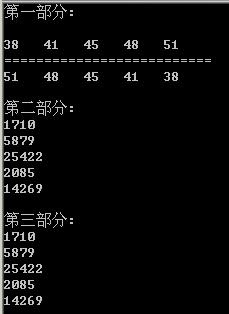
由此可见, 利用不同的随机数种子产生的随机数是不同的, 而使用相同的随机数种子所产生的随机数序列都是一模一样的. 那既然是随机数,为什么产生的结果又会是一样, 带着这个疑问我们再看看VC6中随机数相关的2个标准库函数的实现:
看了后发现原来rand 函数的实现是基于线性同余法(Linear Congruential Method, LCM) ,主要是利用了如下公式:
Xi+1=(a*Xi+c)mod m;
其中a为乘子(常数),C为增量(常数),X0(i=0时)为种子,m为模.
线性同余法有如下特点:
(1)0≤Xi≤m-1,即Xi只能从0,1,2,……,m-1这m个整数中取值;
(2)适当选择m,a,c,可使Xi产生循环,无论X0取何值,其循环顺序是相同的.其循环周期称为发生器周期,记为P.若P=m,则称该发生器具有满周期. 该类型的函数也被称为线性适配函数(linear congruential function).
利用这种方法可以产生一个周期比较长的各不相同的数所组成的数列,所以在一定的范围里可看成是随机数列. 但是它并不是真正的随机数, 所以一般称之为伪随机数, 可以把它理解为有规律的随机数(感觉很矛盾 ), 而控制这种规律性的最关键的要素就是随机数种子, 所以我们用当前时间做为种子,因为时间是一直在变动的. 那为什么不产生真正的随机数呢,那是因为计算机产生真正随机数方法复杂,实现麻烦,所以C语言用某种数学递推公式来产生伪随机数, 来达到与真正随机数相似的效果. 下面是一个随机数使用例子.
), 而控制这种规律性的最关键的要素就是随机数种子, 所以我们用当前时间做为种子,因为时间是一直在变动的. 那为什么不产生真正的随机数呢,那是因为计算机产生真正随机数方法复杂,实现麻烦,所以C语言用某种数学递推公式来产生伪随机数, 来达到与真正随机数相似的效果. 下面是一个随机数使用例子.
上面所提到的随机数生成器已经能够满足一般的需要了,但是却谈不上完美,事实上它本身还有很多缺点,首先它依赖于种子,它是利用种子计算出随机数,看了代码就知道,上一个随机数是下一个随机数的种子,本身就有很强的规律性,所以很容易遭受攻击,下面就是两起典型的案例:
一. Netscape Navigator浏览器早期版本的攻击可能是最著名的可预测随机攻击,其中用于其SSL(Secure Sockets Layer,安全套接字层)密钥的随机数有着很高的可预测性,使得SSL 失去意义.
二. 另一个就是攻击ASF软件公司的TexasHoldem Poker应用程序.这种'发牌'软件在算法中利用了Borland Delphi的随机函数.这个随机函数的实现类似于上面的rand()函数.
正是因为它有这些缺点,所以大家把此类随机数称为伪随机数,这个'伪'字就带有'规律性'的意思. 那么到底有没有'真正的随机数'呢? 熟悉linux的人就知道,linux内核提供了一个叫/dev/random的接口,通过读取这个接口就可以获取'真正的随机数'. 那它是怎么实现的呢,在内部其实linux维护了一种称为"熵"(entropy)的东西.
那什么是"熵"? 你可以把"熵"理解成一系列的随机因子, 比如用户按键,定时器芯片的误差,空闲时间,中断时间等偶然因素. 正是利用了这些偶然的因素才能产生所谓的'真正的随机数'. 那在windows下面有没有类似的方法?当然有. windows中提供一个API: CryptGenRandom(), 申明于Wincrypt.h. 下面是这个函数使用的一个例子:
随机数生成本身就是一个很深奥的课题, 本文仅仅是粗略的介绍了一下,希望能对新手有所帮助.
| 程序代码: | [ 复制代码到剪贴板 ] |
其中RAND_MAX是一个宏, 值等于 0x7fff, 十进制的32767,这个值是C语言中short类型的最大值. srand是初始化随机数种子(seed)的函数,是以当前时间(time(NULL))为参数, 那随机数种子是什么东西, 为什么要以当前时间为参数, 带着这些问题我们再看一个例子:
| 程序代码: | [ 复制代码到剪贴板 ] |
这个例子的输出结果如图:

由此可见, 利用不同的随机数种子产生的随机数是不同的, 而使用相同的随机数种子所产生的随机数序列都是一模一样的. 那既然是随机数,为什么产生的结果又会是一样, 带着这个疑问我们再看看VC6中随机数相关的2个标准库函数的实现:
| 程序代码: | [ 复制代码到剪贴板 ] |
看了后发现原来rand 函数的实现是基于线性同余法(Linear Congruential Method, LCM) ,主要是利用了如下公式:
Xi+1=(a*Xi+c)mod m;
其中a为乘子(常数),C为增量(常数),X0(i=0时)为种子,m为模.
线性同余法有如下特点:
(1)0≤Xi≤m-1,即Xi只能从0,1,2,……,m-1这m个整数中取值;
(2)适当选择m,a,c,可使Xi产生循环,无论X0取何值,其循环顺序是相同的.其循环周期称为发生器周期,记为P.若P=m,则称该发生器具有满周期. 该类型的函数也被称为线性适配函数(linear congruential function).
利用这种方法可以产生一个周期比较长的各不相同的数所组成的数列,所以在一定的范围里可看成是随机数列. 但是它并不是真正的随机数, 所以一般称之为伪随机数, 可以把它理解为有规律的随机数(感觉很矛盾
| 程序代码: | [ 复制代码到剪贴板 ] |
上面所提到的随机数生成器已经能够满足一般的需要了,但是却谈不上完美,事实上它本身还有很多缺点,首先它依赖于种子,它是利用种子计算出随机数,看了代码就知道,上一个随机数是下一个随机数的种子,本身就有很强的规律性,所以很容易遭受攻击,下面就是两起典型的案例:
一. Netscape Navigator浏览器早期版本的攻击可能是最著名的可预测随机攻击,其中用于其SSL(Secure Sockets Layer,安全套接字层)密钥的随机数有着很高的可预测性,使得SSL 失去意义.
二. 另一个就是攻击ASF软件公司的TexasHoldem Poker应用程序.这种'发牌'软件在算法中利用了Borland Delphi的随机函数.这个随机函数的实现类似于上面的rand()函数.
正是因为它有这些缺点,所以大家把此类随机数称为伪随机数,这个'伪'字就带有'规律性'的意思. 那么到底有没有'真正的随机数'呢? 熟悉linux的人就知道,linux内核提供了一个叫/dev/random的接口,通过读取这个接口就可以获取'真正的随机数'. 那它是怎么实现的呢,在内部其实linux维护了一种称为"熵"(entropy)的东西.
那什么是"熵"? 你可以把"熵"理解成一系列的随机因子, 比如用户按键,定时器芯片的误差,空闲时间,中断时间等偶然因素. 正是利用了这些偶然的因素才能产生所谓的'真正的随机数'. 那在windows下面有没有类似的方法?当然有. windows中提供一个API: CryptGenRandom(), 申明于Wincrypt.h. 下面是这个函数使用的一个例子:
| 程序代码: | [ 复制代码到剪贴板 ] |
随机数生成本身就是一个很深奥的课题, 本文仅仅是粗略的介绍了一下,希望能对新手有所帮助.